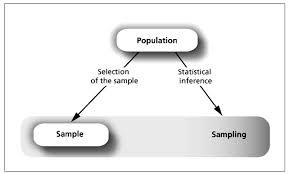
Statistical theory is a very general concept which serves to elucidate the origin of other statistical practices. For example, the practices of statistical inference, mathematical statistics, probability and statistical decision-making, are all based from the framework of statistical theory.
Furthermore, the study designs and data analyses practiced by researchers and statisticians are techniques which satisfy the principles of statistical theory. Similarly, comparisons can be generated between data sets because statistical theory provides the necessary guide required for comparing data. Evidently, statistical theory is a part of all areas of statistics which involve analyzing, describing, and using data to create conclusions and formulate future decisions.
Statistical theory provides the rationale for the full range of steps involved in statistical analyses. The techniques of modelling, data collection, summarising data and interpreting data are all based from statistical theory. For example, in terms of summarising data, the principles of statistical theory account for the different ways which data can be summarised and which aspects of the data should be summarized. Additionally, statistical theory addresses how well a limited sample size can describe a data set.
Clearly, in the study of statistics, statistical theory has many applications and therefore, allows statistics to extend beyond pure mathematics and connect research with the real world. It is through statistical theory that predictions and/or conclusions can be made from data sets, which is the general objective of statistical inference. Furthermore, it allows researchers to attempt to answer problems and explain cause-and-effect phenomena. Thus, it is also linked to the subjects of Bayesian inference and general estimation.
© BrainMass Inc. brainmass.com June 30, 2024, 9:26 am ad1c9bdddf