Credible Interval

A credible interval, also referred to as a Bayesian probability interval, represents the probability domain around the posterior moment. This probability domain represents the region in which a fixed value will be found a certain percentage of the time. The following expression is representative of a two-sided posterior distribution in which the two tails are of equal probability (1):

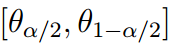
Figure 1. This interval presents the two end points of the posterior distribution (θ).

For example, consider a population with a mean female weight of 140 pounds and a credible interval of 95% for the interval of 135 – 145. In this case, the value of alpha is 5% and 2.5% is represented by each tail of the distribution. This credible interval represents that 95% of this female population of interest falls within this interval of 135 – 145 pounds.

A credible interval parallels the concept of a confidence interval for frequentist inferences. However, these two intervals are rather different. For one, a credible interval includes information from the prior distribution, whereas a confidence interval is only based on the current information. Additionally, confidence intervals are based on repeated sampling.

Secondly, both of these intervals treat nuisance parameters differently. A nuisance parameter is a value which is not currently of interest, but is included in the analysis with all of the other values of interest. For instance, the variance of a normal distribution is an example because with the normal distribution, the mean is of the most concern.

Evidently, credible intervals and confidence intervals have different interpretations. Nevertheless, each specific interval is most appropriate in a particular case, with credible intervals being the requirement when working with the Bayesian inference.

Reference:

1. http://www.stat.tamu.edu/~fliang/STAT605/lect01.pdf

BrainMass