Theoretical computer science is a division of general computer science and mathematics which focuses on the abstract and mathematical aspects of computing. The field of theoretical computer science is interpreted broadly to include algorithms, data structures, computational complexity, distributed computing, parallel computing, and quantum computing. Work in this field is often distinguished by its emphasis on mathematical technique and formal proofs.
Formal algorithms have existed for many years. However, it was not until 1936 when Alan Turing, Alonzo Church and Stephan Kleene formalized the definition of an algorithm. These developments have led to the modern study of logic, computability and computer science as a whole. Now the filed is abuzz with talk of the future of quantum computing, the most exciting potential future path that modern computing might take.
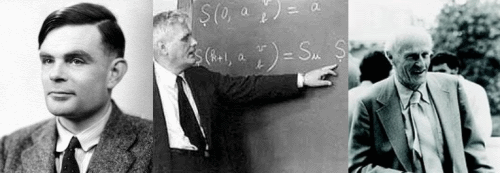
Turing, Church (credit: Princeton University, Institution of Mathematics) and Kleene (credit: Konrad Jacobs, Erlangen)
The most important fields of theoretical computer science, and accordingly, those most often taught and studied, are as follows:
- theory of computation, including automata, computability and computational complexity theories
- programming language theory
- compiler theory
- artificial intelligence




