An automaton is something which processes input according to a pre-determined set of instructions. In computer science, these instructions are coded in, and can allow the automaton to perform a variety of functions as long as the input is of a certain form that it can 'understand'. As automata are extremely useful for problem-solving, they are used widely in computer science to reduce infinite sets to finite representations that can be handled, thus making the sub-field of automata theory a highly important one.
Automata enjoy the most common use as tools to solve problems in formal languages as they are able to understand and process any subset of the input set they were built for. They often represent and recognise entire languages, and process them using various states that can be shown as diagrams for the simplest cases. For this reason, they are often described as state machines. Automata have been used/are being used to find the most efficient solutions to many problems in a relatively uncomplex way, for example:
- emptiness checking
- determinization
- minimization of languages
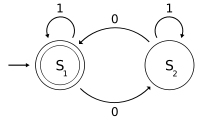
Example of an automaton diagram where the input recognised is {0, 1} and the circles represent states
In addition, automata theory encompasses the less practical, and sometimes borderline philosophical, aspects of automaton computing as well. It brings up questions about the construction and purpose of artificial languages, about their recognizability, closure and hierarchy, and about what sets languages and classes of languages apart.
© BrainMass Inc. brainmass.com July 26, 2024, 4:33 am ad1c9bdddf