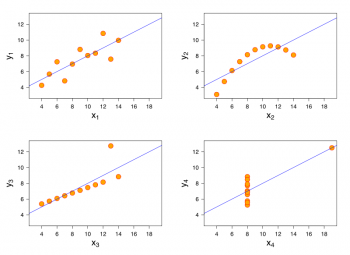
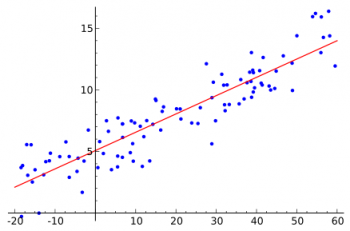
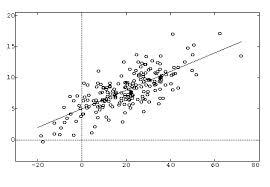
Regression analysis involves identifying the relationship between a dependent variable and one or more independent variables. A model of the relationship is hypothesized, and estimates of the parameter values are used to develop an estimated regression equation. Various tests are then employed to determine if the model is good. If it is, the estimated regression equation can be used to predict the value of the dependent variable given values for the independent variables.
Dependence refers to any statistical relationship between two random variables or two sets of data. Correlation refers to any broad class of statistical relationships involving dependence. Correlations are useful because they can indicate the predictive relationship that can be exploited in practice. Statistical dependence is not sufficient to demonstrate the presence of such a causal relationship.
Correlation and regression analysis are related in the sense that both deal with relationships among variables. The correlation coefficient is a measure of linear association between two variables. The correlation coefficient is a measure of linear association between two variables. Values of the correlation coefficient are always between -1 and +1. Neither regression nor correlation analysis can be interpreted as establishing case-and-effect relationships. They can indicate only how or to what extend variables are associated with each other.
© BrainMass Inc. brainmass.com June 30, 2024, 9:24 am ad1c9bdddf