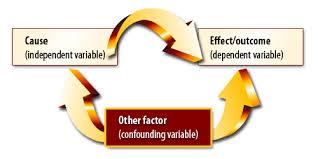
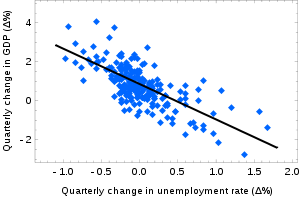
Correlation is the broad class of statistical relationships involving dependence. Dependence is the relationship between two random variables or two sets of data. Examples of dependent phenomena include the correlation between the physical statures of parents and their offspring and the correlation between the demand for a product and its price. Correlations are useful because they can indicate a predictive relationship that can be exploited in practice. Correlation does not imply causation.
Rank correlation coefficients measure the extent to which, as one variable increases, the other variable tends to increase, without requiring that increase to be represented by a linear relationship. If, as the one variable increases, the other decreases, the rank correlation will be negative. It’s common to regard these rank correlation coefficients as alternatives to Pearson’s coefficient less sensitive to on-normality in distributions.
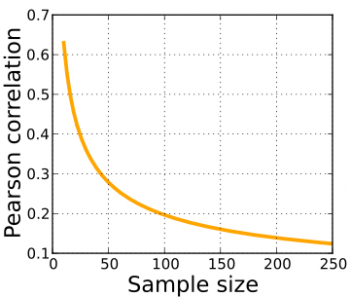
The information given by a correlation coefficient is not enough to define the dependence structure. The correlation coefficient completely defines the dependence structure only in very particular cases. For example, when the distribution is a multivariate normal distribution. Distance correlation and Brownian covariance were introduced to address the deficiency of Pearson’s correlation that it can be zero for dependent random variables; zero distance correlation and zero Brownian correlation imply independence. The correlation ratio is able to detect almost any functional dependency ad the entropy-based mutual information, total correlation and dual total correlation are capable of detecting even more general dependencies.
© BrainMass Inc. brainmass.com June 30, 2024, 12:09 am ad1c9bdddf