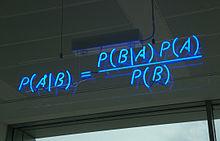Probability is a measure of how likely it is for an event to take place. Probabilities are often denoted by a value ranging between 0 and 1, where 0 represents an impossible event, while 1 represents an event that will definitely happen. Therefore, in this context, the higher the degree of probability, the more likely the event is going to happen.
Before the probability of an event can be computed/measured, the sample space, denoted by the sign Ω, represents the set of all possible outcomes of a random variable. Events in probability are usually denoted by a letter. So for a given set of outcomes, the event may be labeled ‘A’; for another given set of outcomes, the event may be labeled ‘B’. In light of this, an event, either ‘A’ or ‘B’ is a subset of the sample space.
In probability, there are other symbols used to describe composite events. The ∪ sign in A ∪ B denotes the union of two events. So A ∪ B denotes a composite event that occurs if either A or B occurs, or they both occur. The ∩ sign in A ∩ B denotes the intersection of two events. So A ∩ B denotes a composite event that occurs if both A and B occur. The A’ sign denotes an event that cannot occur with A. But one of A’ and A must occur.
These concepts are used widely in an ever expansive area of study, such as mathematics, statistics, epidemiology and even philosophy. Thus, understanding the concepts of probability may prove to be a practical tool for anyone.
© BrainMass Inc. brainmass.com June 30, 2024, 9:20 am ad1c9bdddf