Conditional Probability Distribution

A conditional probability distribution occurs when you have two random variables that are jointly distributed. This means that if we have two variables A and B, knowledge of one of the two variables will give some knowledge of the other variable. Then, the conditional probability distribution is the probability distribution function of one of the two variables given the other variable. For example, the probability of A equal to any 'a' given B = b would be described by the following:

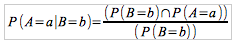
This is the case for discretely distributed values of A and B. If instead, the distribution was continuous, then we would have to use the conditional density function. In which case you would get:

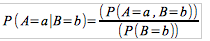
Where the numerator gives the joint density between A = a and B = b, and the denominator is the marginal density.

BrainMass Solutions Available for Instant Download

Prostate Cancer Test

According to a 2018 article in Esquire magazine, approximately 70% of males over age 70 will develop cancerous cells in their prostate. Prostate cancer is second only to skin cancer as the most common form of cancer for males in the United States. One of the most common tests for the detection of prostate cancer is the prostate-

Probability Questions 2B

11. Which probability is greater? A: Prob (person is a CEO of a company | person is a male). B: Prob (person is a male | person is a CEO of a company) a. A b. B c. equally likely 12. The number of raisins in boxes of cereal is normally distributed with a mean of 112 and a standard deviation of 15 raisins. Using

Petro-Co: Solving with the conditional probability formula

Petro-Co must determine whether they should drill an exploratory well. It costs $200,000 to drill, and if oil is discovered, the value (net profit) is estimate to be $800,000. If oil is not discovered, the cost will be just a loss for Petro-Co. Currently there is a 45% chance that drilling a well will lead to oil discovery.

Case Study: Martin-Pullin Bicycle Corporation

This is an inventory control model issue. I need help on the attached case study and be able to answer the case study questions with an Excel spreadsheet. Martin-Pullin Bicycle Corporation Martin-Pullin Bicycle Corp. (MPBC), located in Dallas, is a wholesale distributor of bicycles and bicycle parts. Formed in 1981 by cou

Hypothesis Testing 20 questions

Question 1 of 20 1.0 Points Results from previous studies showed 79% of all high school seniors from a certain city plan to attend college after graduation. A random sample of 200 high school seniors from this city reveals that 162 plan to attend college. Does this indicate that the percentage has increased from that of previou

Standard normal distribution and empirical rule

Probability, Sampling Distributions, and Inference 1) If light bulbs have lives that are normally distributed with a mean of 2500 hours and a standard deviation of 500 hours, what percentage of light bulbs have a life less than 2500 hours? 2) The lifetimes of light bulbs of a particular type are normally distributed with

How Many People to Survey?

How Many People to Survey? Poll results are prevalent in the media, especially leading up to elections, as are reports on surveys done by universities and research groups. The survey results of small groups of people are used to portray a general consensus about a population. Do you ever wonder how many people should be in

Exercises for improving flexibility in each joint in the body

I need assistance solving these problem exercises in excel format. CHAPTER 8 EXERCISE 2 The following is a list of 29 hospitals in the Cincinnati (Ohio) and Northern Kentucky region. The hospitals are identified by numbering them 00 through 28. Also included is whether the hospital is a general medical/surgical hospital (M/S

Normal distribution and normal approximation

[1] A particular airline has 10:00 a.m. flights from San Francisco to New York, Atlanta, and Miami. The probabilities that each flight is full are 0.60, 0.40, and 0.50 respectively, and each flight is independent one another. a) What is the probability that all flights are full? b) What is the probability that only the New Yo

Merit for a Lawsuit: Sexually Discriminatory Hiring Practices

The (entirely fictitious) University of South Central Maryland (USCM) is being sued for sexually discriminatory hiring practices. Last year, they hired two classes of employees: administrative staff and academic staff. They received 750 applications from women for administrative staff positions, of which they hired 250, and 2

Constructing the 99% confidence interval for the population mean

In a study of factors affecting soldiers' decisions to reenlist, 64 subjects were measured for an index of satisfaction and the sample mean is 60 and the sample standard deviation is 16. Use the given sample data to construct the 99% confidence interval for the population mean.

Perform a Hypothesis Test Using t Distribution

The medium size serving frozen yogurt has an average of 4 ounces. A random sample has 14 servings with a mean of 4.31 ounces and a standard deviation of 52 ounces. I need to do a test with α = .05 as the claim. Find the p-value for the test. There is a normal distribution of weight per serving.

Computing probability using normal distribution

The diameter of small Nerf balls manufactured at a factory in china is expected to be approximately normally distributed with a mean of 5.2 inches and a standard deviation of 0.08 inches. suppose a random sample of 20 balls are selected, what percentage of sample means will be less than 5.15 inches?

finding probability using standard normal distribution in a real life example

Suppose that the waiting time for a license plate renewal at a local office of a state motor vehicle department has been found to be normally distributed with a mean of 30 minutes and a standard deviation of 8 minutes. what is the probability that a randomly selected individual will have a waiting time between 15 and 45 minutes

Interval Construct/Estimate a Population Mean/Estimate the Value of a Parameter

22. You Explain It! Superstition A USA Today/ Gallup poll asked l006 adult Americans how much it would bother them to stay in a room on the 13th floor of a hotel. Interestingly, 13% said it would bother them. The margin of error was 3 percentage points with 95% confidence. Which of the following represents a reasonable interpret

Difference Between Discrete and Continuous Variables

Please help me calculate the following: a. The number of defects in a roll of carpet b. The distance baseball travels in the air after being hit c. Number of points scored during a basketball game d. square footage of a house

Calculating probability under a standard normal curve

We are estimating the spares requirement for a radar power supply. The power supply was designed with a mean (μ) life of 6500 hours. The standard deviation (σ) determined from testing is 750 hours. What is the likelihood that a power supply would fail in less than 4880 hours?

Calculating probability that a stock gained value and lost value

The major stock market indexes had mixed results in 2011. The mean one-year return for stocks in the S&P 500, a group of 500 very large companies, was 0.00%. The mean one-year return for the NASDAQ, a group of 3,200 small and medium-sized companies, was -1.8% Historically, the one-year returns are approximately normally distribu

Statistics: Conditional Probability

Assume three buckets. Bucket 1: 6 red and 4 black balls Bucket 2: 8 red and 2 black balls Bucket 3: 4 red and 1 black ball Draw a ball from number 1: if red go to number 2; if black go to number 3. 1. What is probability (red on draw 2, given red on draw 1)? 2. What is probability (black on draw 2, given red on draw

Using the Normal Approximation to the Binomial

According to study done by Nick Wilson of Otago University, the probability a randomly selected individual will not cover his or her mouth when sneezing was 0.267. Suppose you sit on a mall bench and observe 200 people pass by as they sneeze. 1) Use the normal approximation to the binomial to find the probability of observing

Poisson distribution and other probability tests

PROBABILITY Question 1 A company employs 400 salespeople. Of these, 83 received a bonus last year, 100 attended special training program at the beginning of last year, and 42 both attended the special sales training and received a bonus. (Note: Bonus was based totally on sales performance.) a) What proportion o

Type I error of Hypothesis Testing

A traffic accident has occurred. Witnesses report that Car A ran a stop sign and collided with Car B. The driver of Car A was arrested based on the charge of running the stop sign. At the trial, the jury found the driver of Car A guilty as charged. Based on additional evidence that was obtained after the trial, it was determi

Conditional Probability Relationships

As a part of your proposals. You need to submit demographic information to help demonstrate that the location chosen by the management teams will be a good investment. You have collected the following data sample of 2000 customers (specifically. the person paying the bill) on age and gender. (Please note: The bins used were dict

Conditional Probability: Population Obesity and Teenage Pregnancies

1.a) Overweight? Choose an American adult at random. Define two events: A= the person chosen is obese B= the person chosen is overweight but not obese According to the 2007 National Health Interview Survey, P(A)=0.26 and P(B)=0.35. Explain why events A and B are disjoint. 1. b) Say in plain language what th

Endometriosis

Approximately 4% of females above the age of 16 have endometriosis. A) If 10 females are randomly selected from the population, what is the probability that 2 will have this condition? B) If 10 females are randomly selected from the population, what is the probability that at most 4 will have this condition? C) If 50

statistics

A box contains six parts. Two of the parts are defective and four are ok. If three of the six parts are selected from the bin, how large is the sample space? Which counting rule did you use, and why? For this sample space, what is the probability that exactly one of the three sampled parts is defective? A business has 20 emp

Caterpillar Corporation

The Caterpillar Corporation depicts the current status for various classifications of equipment used in a Caterpillar manufacturing plant. The company categorizes equipment usage as Low, Medium, or High, depending upon the number of expected manufacturing applications applicable to its use. Equipment is also subject to availabil

Conditional Probability for efficacy of three drugs to treat headaches

See attached file for table. Which Probability formula should be used? Please explain. A researcher wants to prove the efficacy of three drugs to treat headaches. Results are given in the following table. If one of these subjects is randomly selected: 12- Find the probability that the subject had a headache given that

Calculating Conditional and Unconditional Probabilities

The probability of having disease X in the general population is only .05. The Sagman Test is a newly discovered method for early detection. Of those who have disease X, the test indicates the disease for 90% of them. Of those who do not have the disease, the test indicates no disease for 90% of them. Is the test a good predicto

Probability and Statistics: For three types of real estate, which has highest EMV?

In a survey done by the local Better Buy store, questions were asked of 300 households that actually purchased big-screen televisions. The table at left indicates the consumer's responses to whether the television purchased was a plasma screen and whether they also purchased a DVR in the past 12 months. Q-1a: What is the p