A cumulative distribution function (CDF) is a distribution function for a random variable X that gives the probability that it will be less than or equal to a value x. That is to say that the cumulative distribution function can be defined formulaically as:
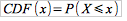
An example of a CDF graph would look like such:
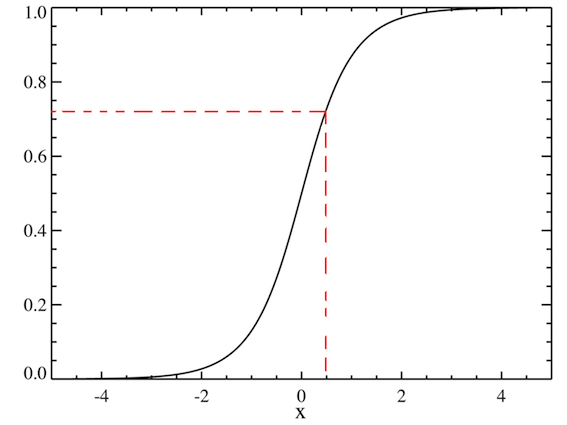
For example, if we were to ask for CDF(0.5), we would find that it is equal to approximately 0.72 as shown by the dotted red line. This means that the probability for the variable X to be less than or equal to 0.5 is 0.72. Consequently the final point on the CDF will always be equal to one, because it is the probability that X will be less than or equal to its maximum value; the answer must be 100%. CDF's can be used to answer questions such as "What is the chance I will get at least 70% on this test? at least 80%? 90%?"
© BrainMass Inc. brainmass.com June 30, 2024, 9:24 am ad1c9bdddf
