Bayesian probability is a different way of looking at the concept of probability. In Bayesian thinking, the probability of an event is not fixed, it is in fact just a quantification of your personal belief. Thus, it is only rational for you to 'update' and change what you believe to be the probability of an event whenever new evidence arrives. Bayesian probability largely relies on Baye's theorem, which can even be applied sequentially until a solution is arrived at. Here is the formula for the probability of event A occurring given event B has occurred:
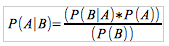
Here is an example of Bayesian updating with Baye's theorem in action. Consider a population with 1% of people have HIV. Take one person and you would assume that there is a 1% chance he has HIV. Now imagine there is an HIV test that is 99% accurate and this person tests positive. An incorrect updating of probability would say that this person has a 99% chance of having HIV. Instead it should look like this:
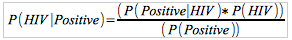
What is the chance that someone tests positive given he has HIV? 99%.
What is the chance that someone has HIV? 1%
What is the probability that someone tests positive? Someone would test positive if they were in fact HIV positive and the test registered accurately (1% * 99%) or if they were in fact HIV negative and the test performed inaccurately (99% * 1%)
So you get:

Bayesian updating shows that this person will only have HIV with probability 50%!
© BrainMass Inc. brainmass.com June 30, 2024, 9:22 am ad1c9bdddf