Partition of Variance

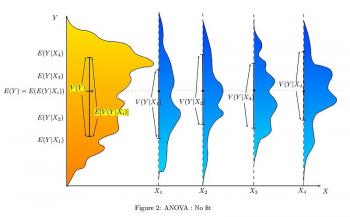
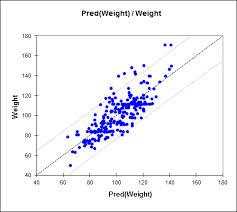
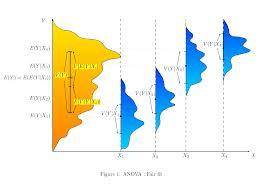
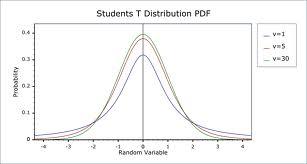
The variance is a measure of how far a set of numbers is spread out. It is one descriptor of a probability distribution, describing how far the numbers lie from the mean. It forms part of a systematic approach to distinguishing between probability distributions. The variance is a parameter describing in part either the actual probability distribution of an observed population of numbers.

The variance of a random variable is its second central moment, the expected value of the squared deviation from the mean μ = E[X]

This definition encompasses random variables that are discrete, continuous, neither or mixed. The variance can also be thought of as the covariance of a random variable with itself.

Var(X) = E[(X – μ)^2]

A formula often used for deriving the variance of a theoretical distribution is as followed:

Var(X) = E(X^2) – (E(X))^2

This formula is also sometimes used in connection with the sample variance. The delta method uses second-order Taylor expansions for the moments of functions of random variables.

Testing for the equality of two or more variances is difficult. The F test and chi square tests are both sensitive to non-normality and are therefore not recommended for this purpose.