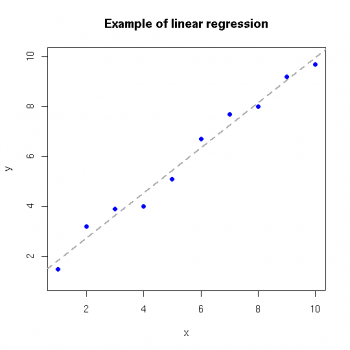
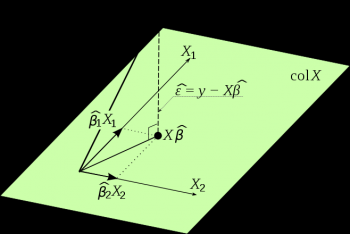
Linear regression is an approach to model the relationship between a scalar dependent variable y and one or more explanatory variable denoted X. The case of one explanatory variable is called simple linear regression. For more than one explanatory variable, it is called multiple linear regressions. In linear regression, data is modeled using linear predictor functions, and unknown model parameters are estimated from the data. Such models are called linear models.
Linear regression was the first type of regression analysis to be studied rigorously, and to be used extensively in practical applications. This is due to the fact models depend linearly on their unknown parameters are easier to fit than models which are non-linearly related to their parameters; also because the statistical properties of the resulting estimators are easier to determine.
Standard linear regression models with standard estimation techniques make a number of assumptions about the predictor variables, the response variables and their relationships. Numerous extensions have been developed that allow each of these assumptions to be relaxed and sometimes entirely eliminated. Numerous extensions of linear regression have been developed, which allow some or all of the assumptions underlying the basic model to be relaxed.
A large number of procedures have been developed for parameter estimation and inference in linear regression. These methods differ in computational simplicity of algorithms, presence of a closed-form solution, robustness with respect to heavy-tailed distributions, and theoretical assumptions needed to validate desirable statistical properties such as consistency and asymptotic efficiency.
Linear regression has many application including biological, behavioral and social sciences. It is used to describe possible relationships between variables. Its ranked as one of the most important tools used in these disciplines.
© BrainMass Inc. brainmass.com June 30, 2024, 9:20 am ad1c9bdddf