Bayesian inference is a process which combines both common-sense and observed evidence in assigning a probability to a statement or belief, even in the absence of a random process. Bayesian inference is one of the two broad categories of statistical inference, along with frequentist inference. However, these two categories are largely different in terms of the fundamental aspects of probability.
Bayesian inference is linked to the concepts of Bayes’ Theorem and Bayesian probability. Bayesian probability allows for uncertainty to be modelled in terms of the outcomes of interest and involves a joining of observable evidence with common-sense knowledge. By combining these two aspects, Bayesian probability helps eliminate some of the complexity associated with the model, such as variables with a meaningless relationship towards the system or unknown relationship which is irrelevant1.
Bayes’ Theorem presents the relationship between two conditional probabilities and is the foundation of Bayesian inference2:
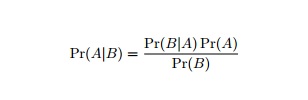
Figure 1. This expression illustrates the conditional probability of A given B. The conditional probability in this case, is also referred to as the “posterior probability”. This is because the conditional probability of event A is being given after a new observation of event B. The prior probabilities of both A and B are being considered along with the conditional probability of B given A.
The concepts: credible interval, prior distribution, posterior distribution, Bayes factors and the maximum a posterior estimator, are all related to Bayesian inference. Further information on these five concepts can be found on the BrainMass website.
References:
1. Cran-r-project. (2014). Bayesian Inference. Retrieved from cran.r-project.org
2. Statisticat, LLC. (2014). Bayes' Theorem. Retrieved from http://www.bayesian-inference.com/bayestheorem
Title Image Credit: Wikimedia Commons