The Maximum a Posteriori Estimator (MAP) is based from the posterior distribution and is representative of a point estimate for an unobserved quantity. This estimate is based from empirical data. Since MAP is a point estimate it is dissimilar to the style of Bayesian statistics which is based on distributions.
Optimizing the prior distribution over the quantity measured is the objective of the maximum a posteriori estimator. MAP is representative of a regularization of the maximum likelihood estimate (MLE). The expression below presents the posterior distribution, which is the distributon MAP aims to maximize.
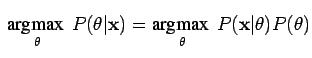
The above function (1) presents two terms. The term on the left-handed side is the posterior distribution. The term on the right side of the expression resembles the product of the likelihood term and the prior term.
The MAP computation differs from that of the MLE because the MLE functions not to maximize the posterior distribution. Rather it maximizes the probability of the data given θ. When working to compute MAP, data needs to be given and assumed to follow a probabilistic model, a particular adjoined distribution (2). In this case, θ is representative of a random variable and the task is to choose a value for θ to resemble where you think the data came from. This is done by choosing a quantity which satisfies the following expression:
ΘMAP = argmax/θ p(θ|D)
The MAP computation is useful because this value is easy to compute and interpret. Furthermore, in contrast to the MLE, it prevents overfitting since it is linked to regularization and it places a prior on θ (2).
References:
- http://www.cs.utah.edu/~suyash/Dissertation_html/node8.html
- http://www.youtube.com/watch?v=kkhdIriddSI
