Bayes Factor

Bayes factor is a method of model selection utilized for trying to determine which model better fits the data of interest when multiple models are being compared by hypothesis testing. It is considered to be an alternative to classical or frequentist hypothesis testing. The concept of Bayes factor was introduced by Harold Jeffreys (1).

Bayes factor is difficult to compute. Nevertheless, it is favoured for hypothesis testing because it avoids model bias; incorporates more uncertainty associated with the model; and favours evidence in support of the null hypothesis (1). The larger a sample size becomes in frequentist hypothesis testing, the more likely it becomes that the null hypothesis will be rejected. This bias is thought to be avoided when using Bayes factor.

When comparing two models, Bayes factor may be approximated as the following ratio (1):

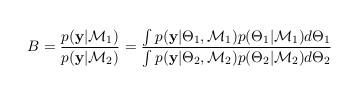
Variables:

B = Bayes factor

p(y|M₁) = marginal likelihood of the data in model 1

p(y|M₂) = marginal likelihood of the data in model 2

In the case where the hypothesis states that model 1 (M₁) is greater than model 2 (M₂), Bayes factor is represented as: (posterior model odds) = (Bayes factor) x (prior model odds) (1). Bayes factor is based on a potentially false ratio, comparing marginal likelihoods.

Furthermore, the computation of Bayes factor can be interpreted based on the following table, in which the value intervals were created by Jeffreys (1):

Thus, the above table illustrates how Bayes factor can be interpreted once computed. Values with limited support, values under 1, support M₂. On the other hand, evidence lending support, favours M₁.

Not all statisticians believe that Bayes factor is useful because it is based on the probabilities of the models with the condition that one must be true (1). Despite this, when appropriate for use, Bayes factor can be calculated to assess model fit and make comparisons between models.

Reference:

http://www.bayesian-inference.com/bayesfactors

BrainMass