Estimation theory is a subset of statistics dealing with the estimation of parameter values from sets having a random underlying component. The measurement of the underlying randomness allows an estimator to be formed, and using these estimators it becomes possible to find a good values for the parameters.
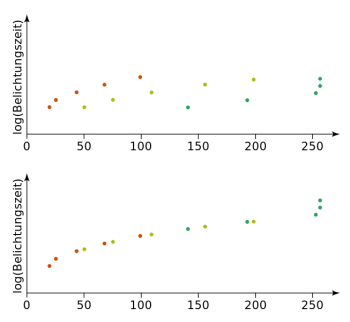
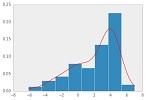
To accomplish this, the data is looked at in a probabilistic way. This assumes that the dataset follows a probability distribution according to the parameters. An example of this is estimating the number of apples an orchid will produce. Knowing that a single tree produces a certain number of apples given certain conditions, it is possible to extend this to a whole orchid by forming a distribution.
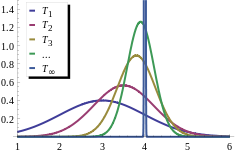
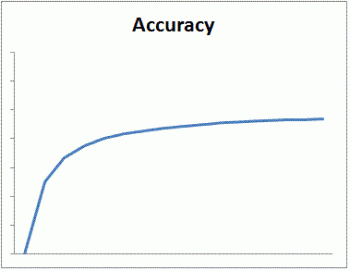
The main goal of estimation theory is to find a good estimator that is dependent on an easy to implement parameter. When completed, the estimator will be a method where one can input data, and it will output the parameter values. When creating estimators, it is also important to ensure they are as optimal as possible. The optimality of an estimator is defined by the amount of average error it has versus all the other estimators for the same or similar problems. The estimator with the least amount of average error is considered to be the optimal estimator for the problem. There is also a theoretically optimal value that can be calculated, but not necessarily achieved in reality, which can be useful for determining optimality.
© BrainMass Inc. brainmass.com June 30, 2024, 9:24 am ad1c9bdddf