Maximum Likelihood Estimation

In statistical modeling, maximum likelihood estimation is a concept which applies to the practice of estimating the parameters of a model. The maximum likelihood estimation is based from the likelihood function, which is a function of unknown parameters (1).

The likelihood function encompasses the idea of how for any function, the outcome variable of a statistical model is distributed to an unknown parameter. This unknown parameter is defined as theta (θ). Furthermore, this outcome variable can either be discrete in its distribution, resembling the probability function, or continuous in its distribution, analogous to the probability density function (1). The likelihood function is utilized in trying to estimate this unknown parameter θ.

With maximum likelihood estimation, what is being calculated is the maximum likelihood estimate or MLE, which is representative of the parameter value where there is the maximal probability according to the observed data (1). The MLE can be calculated using a logarithmic function. In this case, θ is calculated by determining the derivate of the log likelihood function and equaling the function to 0 (1):

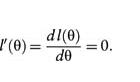
By solving for θ, the maximum likelihood function is being maximized. When given a data set of certain points, it is assumed that these random variables follow some distribution. With maximum likelihood estimation, the goal is to try and estimate the truest value of theta, which represents where the data comes from.

The logarithmic function is utilized because it is easier to work with sums rather than the products.

References:

http://knowledge.sagepub.com.proxy.queensu.ca/view/medical/n213.xml#n213

BrainMass Solutions Available for Instant Download

Mean

You work in the corporate office for a nationwide convenience store franchise that operates nearly 10,000 stores. The per-store daily customer count has been steady, at 900, for some time (i.e., the mean number of customers in a store in one day is 900). To increase the customer count, the franchise is considering cutting coff

Estiation Theory

Let the random variables [x11, ...., xN] satisfy the model xN = theta + w_n; n = 1, ...., N where {w_m} is i.i.d. zero-mean Gaussian of unit variance. Assume now that you cannot access the sequence [xN] but instead you observe the following function of xN yN = sign(xN - T); n = 1, ...., N, where T a is a known constan

Uniform Distribution and Bernoulli Distribution

See the attachment for the fully formatted solution. 1. Let -- be a random sample from a uniform distribution on --. a) Find the MLE --. b) Show that the distribution of -- does not depend on -- and use it to set 1 - alpha confidence interval for --. c) Show that the likelihood rate test statistic -- for testing --- again

Determining the movements of a Rayleigh distribution

A RV X, has a Rayleigh distribution if pdf takes the form fx(x) = x/theta (exp(-x^2/2theta)) where x>0 and theta is positive parameter. We know that E(X) = (theta pie/2) ^1/2, E(X^2) = 2 theta. If the method of moments estimator is such that theta = (2/pie)^1/2 X and maximum likelihood estimator is 1/2n (Sum xi)^2 , how does

Likelihood Function, Maximum Likelihood Estimate (MLE)

1. The number of messages left on your answering machine during 14 successive days are 2, 1, 1, 3, 1, 0, 0, 3, 0, 1, 4, 0, 0, 2.. i) Select a model for this problem. ii) Find the maximum likelihood estimate of the average number of messages left per day on your answering machine in this model for general n and general data. i

Method of Moments Estimator and Maximum Likelihood Estimator

Let X1,...Xn be independent and identically distributed with pdf f(x|theta)=(theta)x^(theta-1) for 0 less than x less than 1 , =0 otherwise i. Name the distribution above and its parameters. ii. Find the method of moments estimator (MME) of theta by finding E(X) and setting it equal to Xbar and solve for the

Maximum likelihood and Fisher information

Suppose x(sub 1), x(sub 2), ..., x(sub n) is a random sample from a distribution with probability density f(x/Î?)=( 1 / (Î?+1)) e^(-x/(Î?+1) where x>0 and Î?> -1 A. Find the maximum likelihood estimator of Î? and show it is unbiased. B. Find the Fisher Information I(Î?). C. Does the variance of the maximum likelih

Construct Unbiased and Maximum Likelihood Estimator - Rayleigh

See attached file. Rayleigh distribution has PDF f(x) = x/(ϴ) e^(-x^2/2ϴ) x>0 0< ϴ<∞ a) It can be shown that E(x2) = 2ϴ, use this information to construct unbiased estimator for ϴ b) Find maximum likelihood estimator ϴ. Compare to a).

Point Estimator for Uniformly Distributed Interval

Question Details: Let X1, X2, ...., Xn be uniformly distributed on the interval (0 to a). Recall that the maximum likelihood estimator of a is â =max(Xi). a) Argue intuitively why â cannot be an unbiased estimator for a. b) Suppose that E(â ) = na /(n+1). Is it reasonable that â consistently underestimates a

First order moments , estimation , estimators

Probability and Statistics I have four problems in the attached file. I would like the solutions to be very detailed as much as possible because this homework will be my review for the midterm. My own solutions are wrong so need someone to help me solve this.... (See attached file for full problem description)

Max Likelihood Methods (Estimators)

Let Y1<Y2<......<Yn be the order statistics of a random sample of size n from the uniform distribution of the continuous type over the closed interval [theta- rho, theta+ rho]. Find the maximum likelihood estimators for theta and rho. Are these two unbiased estimators?