Trigonometry is a field of geometry which focuses solely on measuring triangles in terms of the lengths of their sides and their angles. Interestingly, trigonometry first developed for astronomical studies and has evolved to be used for further applications today such as computer graphics and for medical imaging like CAT scans.
All triangles have three angles and three sides. When given a triangle with only one known side value and two known angle values, trigonometry can be used to calculate the missing values. Trigonometry is a field of geometry inexplicitly linked to the measurement of angles.
There are three functions which are integral to the study of trigonometry which are related to the concept of the Pythagorean Theorem. The Pythagorean Theorem is based on the lengths of a right angled triangle’s sides and is represented by the equation:
a2 + b2 = c2. In this equation, c is equal to the hypotenuse, which is the side opposite from the right angle (90 degrees). The values a and b represent one of the other two sides: a is the side opposite of the hypotenuse and b is the side adjacent to the hypotenuse. Figure 1 represents a right angled triangle.
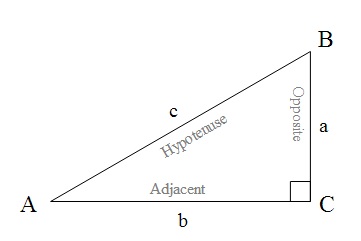
Figure 1. This figure is representative of a right angled triangle and the variables labelled on this triangle correspond with the Pythagorean Theorem and the three trigonometric functions. The lower case letters represent side length values and the capitalized letters represent angle values. This image has been taken from http://commons.wikimedia.org/wiki/File:TrigonometryTriangle.svg.
The three functions integral to the study of trigonometry are as follows (the ratios use the lengths of the sides):
- Cosine Function: This function has the following ratio:
cos A = side adjacent to the hypotenuse/hypotenuse (a/h)
- Sine Function: This function takes the following ratio:
sin A = side opposite from the hypotenuse/hypotenuse (o/h)
- Tangent Function: This function utilizes the following ratio:
tan A = side opposite the hypotenuse/side adjacent to the hypotenuse (o/a)
The mnemonic SOH-CAH-TOA is often taught as a way to remember which function matches with which ratio.
© BrainMass Inc. brainmass.com June 30, 2024, 9:57 am ad1c9bdddf