Searching algorithms are aptly named - each on is a finite set of well-defined instructions to be used as steps for searching a collection of items for a member displaying a specific, desired attribute. These items could be stored in a list, array, dictionary, database or simply be a search space defined by a mathematical formula - or any combination thereof - and the search parameters can also be defined in any number of ways, so constructing an efficient, specially-tailored search algorithm can be challenging.
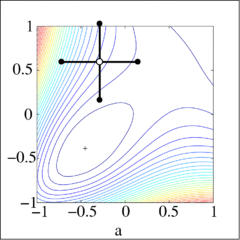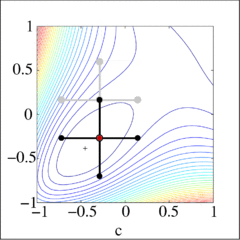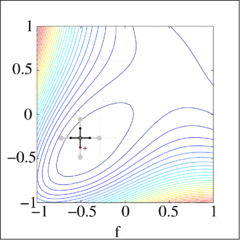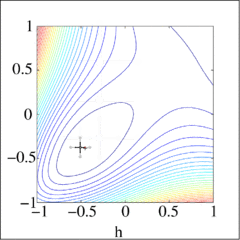
Direct search method graphically displayed on a Broyden function [ Constructed in MATLAB by Guillaume Jacquenot ]
When searching virtual space, search algorithms can be described as a sort of constrain satisfaction problem where the end state is a set of objects that meets some pre-determined constraints or limitations, e.g. all the prime numbers in a set of natural numbers given. These contraints need not be mathematical, however, they could be anything from the qually simple 'all the blue marbles in the marble collection' to a more abstract and hard-to-define, 'all the people in the country fit to lead their nation'. These properties are determined by the machine performing value assignments to chosen variables in order to compare or single out desirable objects.
More technically, search algorithms are commonly constructed on the basis of mathematical equalities or in equalities (e.g. find all the people equal to or taller than 1.5m), or on functions that minimize or maximize a variable (e.g. find the tallest person). A subclass of search algorithms are those whose metaheuristic method involves viewing the items in the collection to be searched as vertices of a virtual graph joined by edges that represent attributes or other heuristic links. These algorithms scan the space by travelling from vertex to vertex via these edges in a special order. On the other hand, collections to be searched may be viewed as a tree. Unlike with a graph, algorithms for searching trees exist that are entirely guaranteed to find the exact or optimal solution if only they are given enough time to execute fully.
Often, instead of searching out a particular single item, a sub-structure of the overall collection may be desired. Combinatorial search algorithms are of paramount use here. Given a discrete structure such as a finite group, string or graph, these algorithms can seek out a sub-structure whose every element displays the desired properties, or otherwise contains a maximum or minimum value of a given function.
© BrainMass Inc. brainmass.com June 30, 2024, 10:10 am ad1c9bdddf