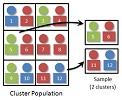
Sampling is utilized in statistics to survey a specific subset of a population as it is often not feasible to collect observations for an entire population. Sampling allows various descriptive statistical measures to be computed and these statistics are then useful in trying to estimate or infer the parameters for the entire population.
When conducting a statistical analysis, sampling basically simplifies the process. If a population contained 1 billion subjects, a researcher would be delusional to assume that all 1 billion individuals could be observed or surveyed. However, with sampling, a smaller portion of the individuals from that population could be analyzed. Then, through the use of inferential statistics, estimations could be made with regards to specific parameters applying to the entire population.
There are a multitude of different sampling techniques which can be employed when analyzing a population. Specifically, the most common sampling methods practiced are cluster sampling, systemic sampling, random sampling, nonprobability sampling, and stratified sampling. All of these sampling practices differ in terms of the criteria they use to collect samples and in certain situations one technique may be preferred over another.
In many cases, sampling needs to be implemented because it is impossible or too difficult to identify every unit in a population. Consider particular animal populations, such as sharks. It is not possible to count every shark residing in an ocean. Therefore, through sampling, statistical analyses can be done on populations of specific shark species and reasonable estimations can be construed regarding their total population size.
Clearly sampling is an integral part of any statistical study. However, sampling requires both resources and time, which are finite properties. Therefore, understanding the array of different sampling methods which are possible and when it is best to perform them is critical to efficient sampling in statistics.
© BrainMass Inc. brainmass.com July 17, 2024, 1:05 pm ad1c9bdddf