Flux comes from the Latin word fluxus which means flow. There are two common uses for the term flux. In the transport phenomena, flux is defined as the rate of flow of a property per unit area. Flux as a mathematical concept also represents the surface integral of a vector field. Both definitions of flux are based heavily on mathematics and differential calculus.
In the transport phenomena there are eight different types of transport fluxes. The eight include: momentum flux, heat flus, diffusion flux, volumetric flux, mass flux, radioactive flux, energy flus and particle flux. Each of these fluxes are vectors at each point in space and have a definite magnitude and direction. For incompressible flows, the divergence of the volume flux is zero.
The surface integral of flux is
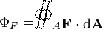
Where
F is the vector field
dA is the vector area of the surface A
The surface normal is directed usually by the right-hand rule. Once can consider the flux the more fundamental quantity and call the vector field the flux density. Often a vector field is frawn by curves following the flow. The magnitude of the vector field is then the line density. The flux through a surface is the number of lines.
© BrainMass Inc. brainmass.com June 30, 2024, 10:14 am ad1c9bdddf