A box plot, also referred to as a box and whisker plot, provides an illustrative representation of the differences between groups by graphing the numerical data for each group using quartiles. Essentially, a box plot represents a way of presenting the first, second and third quartiles. As the title implies, a box plot figure is composed of rectangular boxes and it also includes lines which extend from the box (which represent the whiskers) to illustrate the spread of the data. Figure 1 below presents an example of a box plot for an ecology based study.
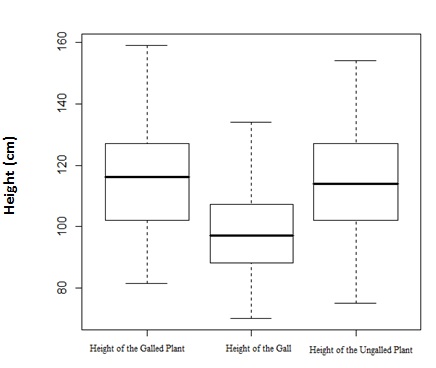
Figure 1. This is a box plot which displays the height variable data for the galled plants, the gall and the ungalled plants (note that the height of the gall is a measurement taken from the ground to the bottom of the gall structure). The black bars in the box structures represent the median value, the bottom line of the box to the black line represents the first quartile and the black line to the outer box line represents the third quartile. The dashed line extended vertically from the box (both on the bottom and the top) to the solid horizontal line, represents the extent of the area where outliers are found.
As described in the figure caption, the rectangular boxes present all three quartiles. Note that the first quartile is equivalent to the 25th percentile, the second quartile is equal to the median or 50th percentile and the third quartile is analogous to the 75th percentile. Thus, box plots are very useful statistical figures, specifically when wanting to graph the median and the entire spread of the data.
In comparison to other statistical figures, box plots provide a method of comparing the variation which exists in a data set which is comprised of more than one independent variable. Although a box plot can be used for only one variable, it is often used to present numerous related variables on the x-axis at one time. Box plots are commonly used in the study of statistics and understanding how to interpret them is an important skill.
© BrainMass Inc. brainmass.com June 30, 2024, 10:16 am ad1c9bdddf