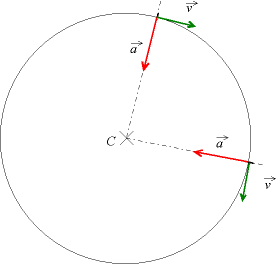
Circular motion is the movement of an object along the circumference of a circle or rotation along a circular path. It can be uniform or non-uniform with the rate of rotation. Due to the object’s constantly changing direction of the velocity vector, the object undergoes acceleration by a centripetal force. Without the acceleration, the object would move in a straight line according to Newton’s laws of motion.
Velocity is tangent to the circular path. No two velocities point in the same direction. The object may have constant speed, but the direction is always changing. For a path of radius r, and where the angular rate of rotation is ω, velocity is defined as:
v= rω
Thus velocity is constant at the same angular rate of rotation. Acceleration of circular motion is defined as:
a= v^2/r
Non-uniform circular motion is where the object is moving in a circular path has a varying speed. The tangential acceleration is non-zero however, the speed is changing. Due to the non-zero tangential acceleration, there are forces that act on an object in addition to the centripetal force. These forces can include weight, normal force and friction.
© BrainMass Inc. brainmass.com June 30, 2024, 9:24 am ad1c9bdddf