Because options confer rights, but not obligations, to the party that holds the option, this party is willing to pay an "option premium" to the writer of the option. This premium reflects the value of the option's rights. But how much is an option worth? We start to explore the value of options by looking at the most amount, and the least amount, investors would be willing to buy a call or a put.
Upper Bounds
Upper Bound of a Call Option
Both American and European call options give investors the right to buy a stock for a specified price. As a result, if a call option costs more than the underlying stock, an investor would simply buy the stock itself.
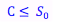
Upper Bound of an American Put Option
American put options give investors the right to sell a stock for a specified price (the strike price) at any time up until the expiry date. As a result, an investor will not buy a put option that is priced higher than the strike price of the option. For example, an investor would not pay $60 for an option that gives her the right to sell a stock for only $50.
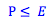
Upper Bound of European Put Options
European put options can only be exercised at the expiry date. As a result, we calculate the upper bound of the option price equal to the present value of the strike price (found using the risk-free rate). If the strike price was higher than the present value of the strike price, an arbitrageur would sell a put, invest the proceeds, use the payoff at the expiry date to pay the contract, and keep the additional proceeds as profit.
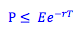
Lower Bounds
Lower Bound of a Call Option
An American call option can be exercised at any time during the life of the option. In this case, the value of the call option cannot be less than the difference between the stock price and the strike price (for options in the money) and zero (for options out of the money). For example, consider a call option with a strike price of $50 is being sold on a stock worth $60. If the option price was less than $10, an arbitrageur would buy the option (for example, at $8), and immediately exercise the option and purchase the stock (at the strike price $50) for a total cost of $58. They could then sell this stock at the market price of $60 and make a risk-free profit of $2.
In fact, we do not have to exercise an American call today. We can also exercise an American call at the expiry date. If we do this, we imagine that the strike price represents a risk-free asset, and we discount this value to find it's present value. If we write the call option today, but do not receive the value of the strike price until a future date, we miss out on investing the proceeds from the call (in, for example, a risk-free bond). For example, consider same stock option with an exercise price of $50 and a current stock price of $60. Wiith a 10% discount rate, that $50 strike price is worth $45 today. If the call option was priced at $10, an arbitrageur would buy the stock option today and invest $45 at the risk-free rate (a total cost of $55). He could also short the stock for $60 today, knowing he will be able to repurchase it, or "cover" it one year from now. This would yield an immediate profit of $5.
Therefore, the lower bound of both an American and a European call option can be found as the difference between the current stock price and the present value of the strike price.
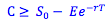
Lower Bound of an American Put Option
American put options have a minimum value of the current strike price less the current stock price. We do not discount the exercise price like we do with American call options. When you exercise a put, you are receiving, rather than paying, the strike price. If you exercised the put today, you could receive $50 and invest it; otherwise, you would just receive $50 at the maturity. Because of the time value of money, exercising a put sooner, rather than later, confers additional benefits to the owner. Therefore, we assume the put is exercised today.
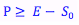
Lower Bound of a European Put Option
European put options must be exercised at the expiry date, so they have a minimum value of the present value of the strike price less the current stock price.
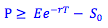
Other Considerations
1. All options cannot have a negative value.
2. American call and put options are always at least as valuable as European ones.
3. American options with more time to maturity are equally or more valuable as corresponding american options with a shorter time to maturity.
Photo by Fabrice Villard on Unsplash
© BrainMass Inc. brainmass.com July 26, 2024, 4:23 am ad1c9bdddf