The signed-rank test is also known as the Wilcoxon signed-rank test which is a nonparametric test, equivalent to the student’s paired t-test, analyzing whether there is a difference between pairs which are not normally distributed. There are many similarities between this test and the Mann-Whitney U test. The way ranking is computed in the Mann-Whitney U test is identical to how it is done in the Wilcoxon singed-rank test. However, in a Wilcoxon signed-rank test, absolute values are ranked because sign does not have an influence on the ranking procedure.
A Wilcoxon signed-rank test requires there to be two nominal data sets which correspond to one categorical variable. In this type of statistical test, the scores come from the same participants. In the Wilcoxon signed-rank test, it is the difference between the pairs which is being tested. So for instance the subjects analyzed may be exposed to a before and after treatment.
For example, a researcher may have wanted to record the weights of 12 individuals before they started a diet and then again, after being on the same diet for 2 months. In this case the sample size is 12.
1. The first step involves writing the null and alternative hypotheses.
Ho = There is no difference in the participant's weight before and after the diet.
Ha = The mean weight before the diet is greater than the mean weight after the diet.
2. Next it is necessary to determine the critical value (Tcritical) using a Critical Value Table. So in this case:
- n (sample size) = 12
- chosen significance level of 0.05
After looking at a Critical Value Table1 the Tcritical value = 13
3. Now it is necessary to draw a table which allows for the calculation of Rank D and Sign Rank D. The ranking system is the same as that used for the Mann-Whitney U test. As well, the paired difference and absolute difference between the before and after treatments need to be calculated first so that the ranking can be completed.
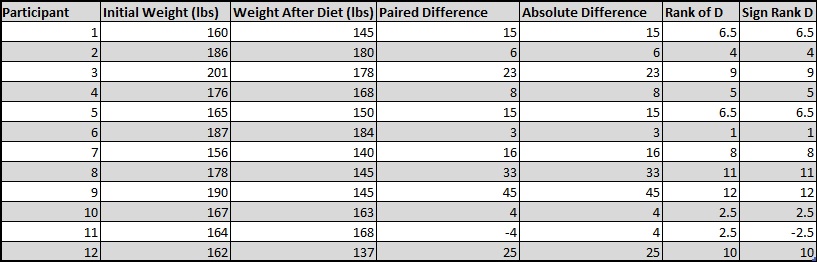
Table 1. This table provided illustrates the necessary calculations for the Wilcoxon signed-rank test. The "Absolute Difference" column requires the computation of the absolute difference, meaning that the value cannot be negative. However, if a paired difference is negative, the negative sign reappears in the "Sign Rank D" column.
4. The calculation of W (which is the sum of all sign rank D values) is the next step. This value gets compared to the Tcritical value.
W = 73
The test statistic (W) is greater than the critical value of 10 and so we reject the null hypothesis.
References:
1. Zaiontz, C. (2013). Wilcoxon Signed-Ranks Table. Retrieved from: http://www.real-statistics.com/statistics-tables/wilcoxon-signed-ranks-table/
© BrainMass Inc. brainmass.com June 30, 2024, 10:07 am ad1c9bdddf