In the study of statistics, the normal distribution is one of the most fundamental concepts and is represented by a graph which is characteristic of a symmetric, bell shaped curve. The normal distribution corresponds to a probability density function which is represented as follows:
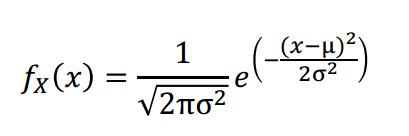
The mean, standard deviation and variance are all measures which are intimately linked to the normal distribution. The centre of the normal distribution curve is equal to the mean, as well as the median and mode. As you move left and right from the centre value width-wise, the standard deviation and variance begin to take on values. For the standard normal distribution, the mean is equal to 0 and the standard deviation equates a value of 1.
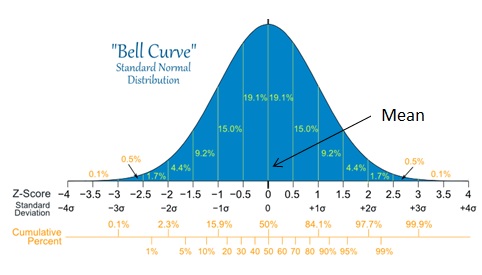
Figure 1. This is a diagram which depicts the bell shaped curve which is characteristic of the standard normal distribution. The mean (μ) is equal to 0 and the standard deviation (σ) equals 1. All the standard deviation values are associated with a percent and the cumulative percentage increases as the standard deviation does.
When considering a random variable, call it x for example, if x has a normal distribution, then it is able to take on any finite value from negative infinity to positive infinity. As is noticeable from looking at Figure 1, 95% of the area lies within 2 standard deviations of the mean. Essentially, the normal distribution represents how in random, natural populations which are normally distributed, 95% of the time the data will not deviate from the mean. This is the basis of the central limit theorem which is another integral concept in statistics.
Furthermore, it is important to note that when dealing with the standard deviation, σ must take on a positive vale. Thus, the variance does as well. Since the variance is the standard deviation squared, this value will always be positive.
The normal distribution is a class of statistical distributions and almost everything done in inferential statistics is based on the normal distribution. When using a normal distribution, the probability of getting a value is represented by a range. Probabilities are computed as areas underneath the distribution curve. The normal distribution is a very important class of statistical distributions and essentially everything done in inferential statistics is based on this continuous probability distribution.
References:
1. The Khan Academy
2. Jbstatistics – Youtube: http://www.youtube.com/watch?v=iYiOVISWXS4
