Explore BrainMass

Explore BrainMass

    Mann-Whitney U

    The Mann-Whitney U-Test is a nonparametric test which is analogous to the student’s two-sampled t-test. This statistical test is utilized to determine if a difference exists between the two samples being compared. The samples do not need to originate from normally distributed populations, but they should come from populations with similar distributions.

    The Mann-Whitney U-Test is conducted using ordinal data, data which is based on rank sums. Since it is a nonparametric test, it analyzes the difference between the medians of two data sets. In addition to utilizing nonparametric, ordinal data, this statistical test should be used when there are more than 5 pieces of data in each sample, but fewer than 20 data pieces in total.

    As with any statistical test, the first step in using the Mann-Whitney U-Test involves setting up the null hypothesis. The null hypothesis in a Mann-Whitney U-Test is always the same. The null hypothesis states that there is no difference between the data sets being compared.

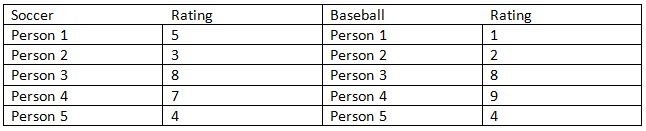
    Example: The enjoyment of watching soccer and baseball was rated among 10 randomly selected individuals aged 20 – 25. Each individual was asked to rate how much they enjoyed watching either baseball or soccer, depending upon which group they were in, out of 10. The results are as follows:

    In a Mann-Whitney U-Test, the data must be ranked. A rank of 1 is given to the lowest rating between the two groups and if there is a tie for a rank between two ratings, that rank and the subsequent rank get averaged. After this is completed, the ranks for each group are tallied. T1 will represent the ranking for soccer and T2 will be the tally for baseball.

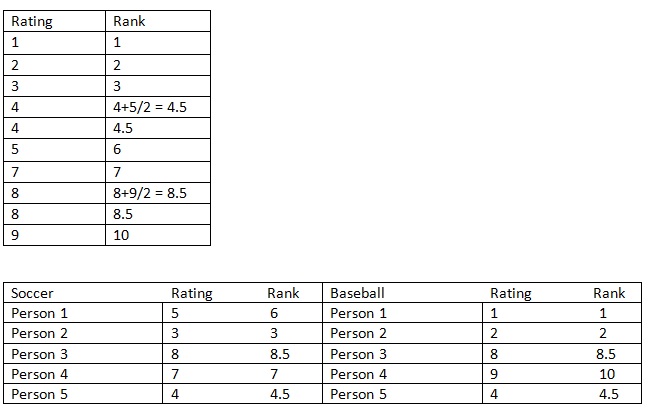
    The ranks are added up to get the values for T1 and T2 (T1 = 29 and T2 = 26).  Then this formula is utilized:

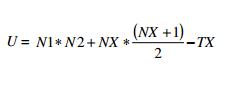
    Variables:

    TX = the larger rank total (the larger rank total of T1 and T2 is used)

    N1 = number of people in T1

    N2 = number of people in T2

    NX = number of people in the larger rank

    Then depending on which significance level is being used, a table giving the critical U values for different sample sizes needs to be used to see whether the derived U value is less or more than is expected at those sample sizes. The null hypothesis is rejected if the U value computed is greater than expected because statistically it is not significant.

    © BrainMass Inc. brainmass.com April 24, 2024, 7:40 pm ad1c9bdddf

    BrainMass Solutions Available for Instant Download

    Non-Parametric Tests: Mann-Whitney Test

    Is there a difference between health service workers and educational service workers in the amount of compensation employers pay them per hour? Suppose a random sample of seven health service workers is taken along with a random sample of eight educational service workers from different parts of the country. Each of their employ

    Mann - Whitney U Test

    Nonparametric Hypothesis Testing Conduct the equivalent, nonparametric test of hypothesis using the five-step process. Perform the five-step hypothesis test on the data. Null Hypothesis: The mean wage of single individuals is equal to the mean wage earned by married individuals. Alternate Hypothesis: The mean wage

    Mann-Whitney Test and Differences in Working Hours

    Use a nonparametric test (attached) to see if there is a difference in hours worked for males and females (variable hrs1). Is there a difference? Explain. The output to analyze is attached. Use a nonparametric test to see if there is a difference in hours worked for males and females (variable hrs1). What do you conclude?

    Nonparametric Hypothesis Testing

    Hypothesis statement: difference in the selling price of a house with a pool (M1) in relation to one without a pool (M2). Based on the research question from which this hypothesis was formulated the numerical and verbal hypothesis is: H₀: M1=M2, or M1- M2 = 0 H₁: M1≠M2, or M1-M2 ≠0 Conduct the

    Non-parametric Hypothesis Tests, Correlation & Regression

    Use the RENAL.sav file from Norusis and do the following: 1) Mann-Whitney U test (nonparametric) - Use the same variables you used in the Independent Samples t-test from DATA ANALYSIS PROJECT 3 (Assignment 11). - Conduct a Mann-Whitney U test on the scale variable with the nominal variable as a grouping variable.

    Practice Problems Using SPSS

    These are practice problems that are mostly Mann Whitney U and Wilcoxsen analysis. 1) Ten monkeys, five reared with a surrogate (artificial) mother and five reared normally, have been observed over a 10-day period in a group play area. The number of self directed behaviors has been scored for each animal during a 20 minute

    Wilcoxon - Mann/Whitney Test

    Please answer in a single short paragraph. 3. Answer a and b in terms of the modern scientific paradigm, a. Which simple linear regression model should be preferred? b. What desirable trait causes it to be the preferred model? a. Intercept = b = 100 Slope = m = 9 R2= 0.4 P value= 0

    Nonparametric Hypothesis Testing Paper

    Stated below is the complete assignment that I have been assigned. I am confused on how to perform Mann-Whitney test the calculation located on page 706. So the null hypothesis would be HO: M1 = M2; and H1: M1 not = M2. included I should State the decision rule and take a sample and arrive at a decision that I am also having t

    Nonparametric testing correlation regression analysis using SPSS

    Mann-Whitney U test (nonparametric) - Using the variables length of stay (scale) variable and Gender (nominal) - Conduct a Mann-Whitney U test on the scale variable with the nominal variable as a grouping variable. - Copy and paste the output in a Word processor in RTF format. - State the hypothesis to be tested.

    Moe's Computer Store: Mann-Whitney U Test

    (10) Moe's Computer Store hired an advertising agency to prepare two advertisements of comparable quality for their new television-computer wristwatch. To see whether both ads led to the same distribution of sales, Moe hired a statistician to find out. Two random samples were taken on 12 months of the first year of sales for

    Analysis of data using SPSS computer program.

    The study is to find out if the analysis of the data supports a smoking ban or not. I have conducted a Mann Whitney, and N-Par test and discovered that the data is skewed. I need to explain what the results mean in a discussion section, and am unsure because the data is a little random. Can you help? column a = id of bar/pub

    Conduct and interpret the appropriate analysis.

    A researcher was interested in the attitudes towards equal rights among stay at home moms and women with jobs outside the home. She creates a survey that measures attitudes toward equal rights, administers it to a sample of 20 women. However, since the survey is not standardizes, she realizes that the scores may not reflect equ

    Wilcoxon-Whitney Test

    What is a Wilcoxon-Whitney Test and when is it used? I am not sure when to use the Wilcoxon-Whitney Test and what it is testing. Can you provide me with this information? Thanks.

    Completing a Non-Parametric Test

    Can you please do a non parametric test (Mann Whitney) on the figures and give me both the full print out of the calculation as well as an APA summary. For the general print out let me know which program you used. You will find a comparison between control and study group on day 1 and 5. I need to know if there has be