The flow to equity (FTE) or free cash flow approach is an alternative capital budgeting approach. The FTE approach simply requires that the cash flows from the project to the equity holders of the levered firm be discounted at the cost of equity capital. There are three steps to the FTE approach:
1. Calculating the levered cash flow
2. Calculating the discount rate for levered equity
3. NPV analysis
1. Calculating the levered cash flow (LCF): The levered cash flow is the cash flows of the project after cash costs, cash paid on interest, and cash paid in taxes. It can also be calculated by adjusting the firm's unlevered cash flows (UCF) by the amount of the after tax interest payment to debtholders.
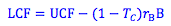
Where,
rB = the interest rate
B = the amount of the project financed by debt
TC = the tax rate
2. Calculating the discount rate for levered equity: The discount rate for levered equity is simply the rate of expected return that can be observed by the stock's price in the market. However, if the leverage of the firm is going to change because of a scale enhancing project, we use the discount rate of the unlevered equity, and adjust it for the new debt:equity ratio of the firm.
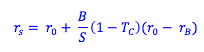
Where,
rs = the levered rate of return
ro = the unlevered rate of return
B/S = the debt to equity ratio
3. NPV analysis: To find the present value of the cash flows to equity, we simply discount the levered cash flows by the expected return of the levered equity. To find net present value, the present value of the initial cash outflows are subtracted.
Unlevered vs. Levered Return to Equity
If it is not given in the question, we can find the expected return to an unlevered firm by taking the observed beta of the levered firm (Bequity), and finding the corresponding beta for the firm if it was all equity (Basset). We can then plot the asset beta on the security market line to find the expected return of the firm if it was all equity.
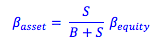
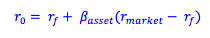
Photo by Dean David on Unsplash
© BrainMass Inc. brainmass.com July 24, 2024, 2:43 am ad1c9bdddf