A circle is a basic shape used in geometry which is representative of a closed curve creating two regions which separate a plane. These two regions are known as the interior and exterior. Additionally, another feature of a circle is that all points are an equal distance from the center.
There are a few measurements which are associated with circles:
- Radius: The radius can be taken from any point on a circle and it is equal to the distance from a point on a circle to the center.
- Circumference: The circumference is equal to the entire distance around a circle following a circle’s edge.
- Diameter: The diameter is a measurement which calculates the distance from one point on a circle directly across to the corresponding point on the other side of a circle. The diameter is twice the value of the radius.
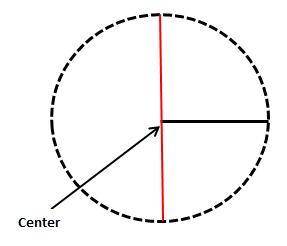
Figure 1. This figure provides an example of a circle. The radius is represented by the black line extending to the center of the circle. The diameter is depicted by the red line which passes through the center of the circle. The circumference is illustrated by the dashed line which acts as the edge of the circle.
Furthermore, the value the concept of pi (∏) is also tightly correlated with the shape of a circle. Pi is always equal to approximately 3.14 and describes the ratio of the circumference to the diameter. Regardless of the size of a circle, this ratio of pi will always be the same.
Thus:
∏ = circumference/diameter
© BrainMass Inc. brainmass.com July 25, 2024, 8:15 pm ad1c9bdddf