Bubblesort

Implementation

Although it's origins aren't easily traced, bubblesort seems to have been around since the early 1960s¹, often under other names like exchangesort and shuttlesort. The following pseudocode shows the basic, unchanged idea:

function bubbleSort(A)         // A is an array to be sorted

n = length(A)

  swapped = true

  while swapped = true

swapped = false // swapped remains false if the algorithm visits                                                     each element with no swaps

for i = 1 to n-1 inclusive

if A[i-1] > A[i] // an element is bigger than the one after it

              swap( A[i-1], A[i] )

              swapped = true

Below is a visual representation of bubblesort performed on the unsorted array [6, 5, 3, 1, 8, 7, 2, 4]. The sorting shown in the graphic is also given in the form of a table to help trace the above code through the process.

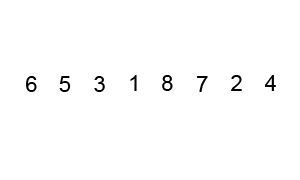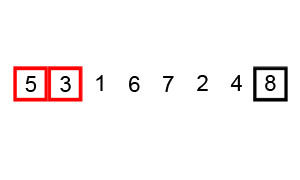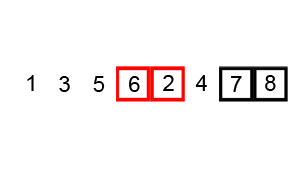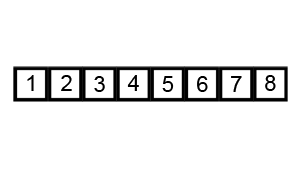
For the table below, bold lettering indicates the numbers that were compared for a given value of i and * shows when a swap was not enacted. The variable 'swapped' remains true as long as at least 1 swap occured over that pass.

Bubblesort passes on an 8-digit array
i	First Pass	Second Pass	Third Pass	Fourth Pass	Fifth Pass	Sixth Pass
1	5, 6, 3, 1, 8, 7, 2, 4	3, 5, 1, 6, 7, 2, 4	1, 3, 5, 6, 2, 4*	1, 3, 5, 2, 4*	1, 3, 2, 4*	1, 2, 3
2	5, 3, 6, 1, 8, 7, 2, 4	3, 1, 5, 6, 7, 2, 4	1, 3, 5, 6, 2, 4*	1, 3, 5, 2, 4	1, 2, 3, 4	1, 2, 3
3	5, 3, 1, 6, 8, 7, 2, 4	3, 1, 5, 6, 7, 2, 4*	1, 3, 5, 6, 2, 4*	1, 3, 2, 5, 4	1, 2, 3, 4*
4	5, 3, 1, 6, 8, 7, 2, 4*	3, 1, 5, 6, 7, 2, 4*	1, 3, 5, 2, 6, 4	1, 3, 2, 4, 5
5	5, 3, 1, 6, 7, 8, 2, 4	3, 1, 5, 6, 2, 7, 4	1, 3, 5, 2, 4, 6
6	5, 3, 1, 6, 7, 2, 8, 4	3, 1, 5, 6, 2, 4, 7
7	5, 3, 1, 6, 7, 2, 4, 8
value of swapped	true	true	true	true	true	false

Notice that bigger numbers should never move left of where they began and smaller numbers never 'bubble' down to the large end of the list at the right.

For the more kinetic learners, this youtube video demonstrates the process through the medium of dance.

Performance

You may have noticed from the above that bubblesort does take some steps to improve efficiency such as 'locking in' the last value at the end of each pass which is always guaranteed to be in it's rightful place and therefore not needed in any further comparisons or swapping. It is also designed so that the workload lessens with each pass, both in iterations and, generally, in the number of swaps required for the pass. However, as demonstrated in the sixth pass above, bubblesort does necessitate a 'useless' pass at the end once the list is fully sorted to ensure no further swaps are needed. In addition, the positioning of the elements plays a heavy role - for larger elements at the front ('rabbits'), it is a fairly swift ride to the back but small elements at the end of the list ('turtles') take a relatively long time to bubble up to the front.

In terms of order, the inner loop runs O(n) operations each time and is called O(n) times, leading to an overall O(n2) rate for bubblesort, much worse than quicksort or mergesort.

For these reasons, and others like them, bubblesort is rarely used in practice, though still widely taught. Donald Knuth writes in his famous book, The Art of Computer Programming, that "the bubble sort seems to have nothing to recommend it, except a catchy name and the fact that it leads to some interesting theoretical problems"².

The comb sort is an enhanced version of bubblesort that seeks to solve some of its problems with turtles, etc. and it runs at a speed comparable to quicksort³.

References:

1. Astrachan, O. (). Bubble Sort: An Archaeological Algorithmic Analysis. [ONLINE] Available at: http://www.cs.duke.edu/~ola/bubble/bubble.html. [Last Accessed 15/04/2014].

2. Donald Knuth. The Art of Computer Programming, Volume 3: Sorting and Searching, Third Edition. Addison-Wesley, 1997. ISBN 0-201-89685-0. Pages 106–110 of section 5.2.2: Sorting by Exchanging.

3. OJ (2008). Sorting Algorithms: The Comb Sort. [ONLINE] Available at: http://buffered.io/posts/sorting-algorithms-the-comb-sort/. [Last Accessed 15/04/2014].

Implementation

Performance

BrainMass