When we discount cash flows from a project, we try to use a discount rate equal to an expected rate of return that is appropriate for the project considering the risks of the project. If a firm's capital structure remains constant, we often use the weighted average cost of capital (WACC) to discount new projects. The WACC is a good approximation of how expensive it is for a business to finance the cost of a new project. For example, if it costs 8% a year to finance a project, it wouldn't make sense to invest in a project that returns less than this 8%.
As a result, sometimes it is beneficial for us to calculate the internal rate of return of a project. Let's say we invest $100 today and make $108 tomorrow, we would have an internal rate of return of 8%. Similarly, if we invested a $100 and made $102 or $110 tomorrow, we would have internal rates of return of 2% and 10%, respectively. The internal rate of return is therefore the rate of return that we use to discount our cash flows so that our discounted cash inflows = our discounted cash outflows.
Recall the definition of net present value: net present value = the cumulative sum of all discounted cash flows. If our discounted cash inflows (a positive number) is the same amount as our discounted cash outflows (a negative number), then the sum of our discounted cash flows must be zero. Therefore, the internal rate of return can be found as the rate of return that, if used, will make the net present value of our project equal to zero.
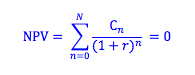
Let's use this in an example. Previously we used an example of an oven that would cost $10,000 to purchase, and would provide $2,500/year in incremental cash flows over its life of five years (see Net Present Value for this full example).
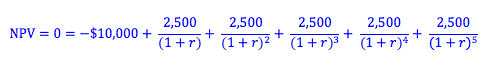
As you might have guessed, finding the proper value for r by using algebra may be quite difficult. Often students use a trial and error method in order to calculate an appropriate value for r. Using an Excel sheet, we can tinker with the rate of return so that we get a sum of cash flows equal to zero. In the above example, we can find an internal rate of return of 7.93% using this method.
When comparing projects, the project with the higher IRR is often preferable. However, IRR does not take in to account the size of the project; for example, a larger project may have a lower IRR but a significantly higher NPV.
CAUTION: IRR treats the interim cash flows from a project as if they were reinvested in another project with the same high rate of return as the IRR. By doing so, the IRR intrinsically "takes credit" for some of the gains from other projects if, or as if, similar projects existed. A more accurate calculation would assume that cash flows from a project are reinvested at the weighted average cost of capital. As a result, the IRR can be significantly OVERSTATED. Similarly, there may be multiple solutions for IRR. Today, the use of the modified internal rate or return (MIRR), which addresses this problem, is becoming much more predominent.
Photo by Pablo García Saldaña on Unsplash
© BrainMass Inc. brainmass.com June 30, 2024, 10:13 am ad1c9bdddf