In a risk-neutral wold, there exists the special case where the expected rate of return on any asset is simply the risk-free rate. This is because investors do not demand any additional return for additional risk. We use this special case for building a risk-neutral binomial option pricing model.
Risk-neutral valuation relies on the intuition that because the actual current price of the stock already balances future expectations for the stock, the value of the option will necessarily reflect this balancing act. That is, an optimist and a pessimist could use any set of probabilities that a stock will go up or down and both arrive at the same present value of the option. Knowing this, we can use the set of probabilities so that the expected rate of return of a stock was equal to the risk-free rate.
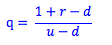
Where q = the risk-neutral probability (that is, the probability of the upstate in a risk-neutral world)
r = the interest rate
u = the value in the up state
d = the value in the down state
We can the find the present value of the call option using this risk-neutral probability. The present value of a call option in a two-state world equals the probability of the upstate times the value of the call option in the upstate, plus the probability of the downstate times the value of the call option in the down state - all discounted to present value.
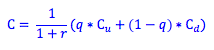
Let's look at the following two state example. Using our first formula, we find the risk-neutral probability (q) using the current stock price of $50 and a risk-free rate of return of 10%.
10% = Probability of the upstate x Stock return in the upstate + (1 - Probability of the down state) x Stock return in the downstate
10% = q * (60-50)/50 + (1-q) * (40-50)/50
10% = q * 20% + (1-q) * -20%
q = 75%
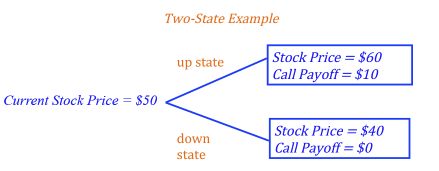
Using our second formula, we can find the present value of the call with a risk-neutral probability of 75%.
C = [(0.75 * $10) + (0.25 * $0)] / 1.10 = $6.82
*This valuation method gives us the same value of the call as we found using delta hedging (see: Binomial Option Pricing Model: Delta Hedging).
Photo by Heather Gill on Unsplash
© BrainMass Inc. brainmass.com July 26, 2024, 4:22 am ad1c9bdddf