A quantile-quantile plot is used when considering whether two populations have a common distribution and is used to analyze these two probability distributions against each other. When comparing these two populations against each other, it is the individual quantiles of each population which are being compared. The term quantile is used to describe a point which lies below a specific fraction or percent, depending on how the value is expressed (1). For example, a quantile of 60% or 0.6 is representative of the point which has 60% of data below it and 40% lying above it.
When constructing a quantile-quantile figure and plotting the individual points, a reference line is drawn at a 45 degree angle. If the majority of the points recorded fall onto or close to this line, this means that both populations being compared are from a normal distribution. In statistics, often times it is critical to know whether populations come from a normal distribution and creating a quantile-quantile plots provides an easy method for finding out.
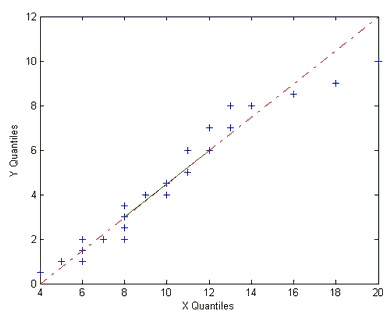
Figure 1 This figure presents a quantile-quantile plot for two different populations. The dashed red line represents the reference line for this plot. A majority of the points from both populations fall upon the reference line. This figure has been taken from: http://www.mathworks.com/help/stats/distribution-plots.html#f14708.
Furthermore, when plotting the two populations, the sample sizes and units of the two populations do not need to be the same for the linear relationship to be accurate. Q-Q plots work with quantiles so the units of both populations get translated to percentages. In statistics, identifying whether populations come from a normally distributed population is an important skill and to further strengthen the results obtained from a Q-Q plot, hypothesis tests can be completed.
References:
(1) http://www.itl.nist.gov/div898/handbook/eda/section3/qqplot.htm
