Cohen’s kappa is a statistical coefficient, identified as k, which deals with independent raters and measures the degree of agreement between them. In measuring the degree of agreement, this statistical measure takes into account the agreement happening by chance. Additionally, statistical significance is rarely associated with the value of k because the magnitude is not usually large enough to be sufficient (1).
The formula used to measure Cohen’s kappa is as follows (2):
k = Pr(a) – Pr(e)/(1 – Pr(e))
Variables:
Pr(a) = relative observed agreement between raters
Pr(e) = hypothetical probability of chance agreement
When using Cohen’s kappa, if the value derived for k is equal to a value of 1.0, this indicates complete agreement between the raters. If k is equal to 0.0, this indicates no agreement between the raters. Additionally, when k = 0, this means that there is no agreement other than what would be due to chance alone.
Cohen’s kappa is a very specific measure utilized in statistics, which is more so related to the practice of probability. It uses a fairly basic equation and requires the calculations for Pr(a) and Pr(e) to be completed. Furthermore, in completing these probability computations, the use of a summary table is an effective method for organizing the required data.
For example: You have 100 people applying for a job at your company. You give the applications to two readers and record the number of times they say “yes” or “no” to an application.
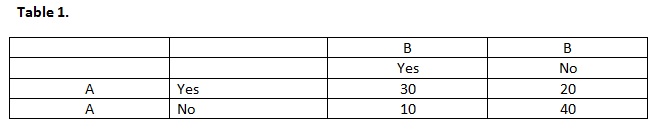
You read Table 1 as follows:
Reader A said yes to 50 applications and no to 50 applications (read across rows).
Reader B said yes to 40 applications and no to 60 applications (read down columns).
How to calculate Pr(e)?
The yes and no counts need to be translated to proportions.
Probability of A and B saying yes = 0.5 (50 applications/100 total application = 0.5) x (0.4) = 0.2
Probability of A and B saying no = 0.5 x (0.6) = 0.3
Pr(e) = 0.2 + 0.3 = 0.5
How about Pr(a)?
Pr(a) = the observed percentage agreement
Therefore, Pr(a) = (30+40)/100 = 0.7. Using Table 1, it can be seen the 30 applications received a from both A and B, and 40 applications received a no from both A and B.
To calculate k, fill in the values for Pr(a) and Pr(e) into the equation.
References:
1. Bakeman, R.; & Gottman, J.M. (1997). Observing interaction: An introduction to sequential analysis (2nd ed.). Cambridge, UK: Cambridge University Press. ISBN 0-521-27593-8.
2. Smeeton, N.C. (1985). "Early History of the Kappa Statistic". Biometrics 41: 795.
