When an investor believes the market is going to go one way or another, he or she will buy or sell options that allow them to profit when the market trend is favorable. However, everyone knows the market is not a sure thing, and even if it is up one day, it could be down the next. As a result, many investors choose to purchase or sell different types of securities - stocks, bonds, futures and options. When these securities are traded at the same time, and relate to the same underlying assets, we call this a trading strategy or option hedging strategy. If done right, an trading strategy will significantly reduce the risk for investors who wish to trade in the derivatives markets. In order to decide what type of securities should be purchased as part of a trading strategy, investors look at the payoffs that buying and selling different options will give them. When an option is purchased, we say an investor is "long an option," in finance talk; when an option is sold, we say an investor is "short an option."
Long an option: If we long an option, we have the right to exercise the option, and we will only exercise the option if it will result in a positive payoff for us. This is the same as buying an option, and we become the holders of the option.
Short an option: If we short an option, the holder of the option has the right to exercise against us. The holder will exercise the option if it will result in a positive payoff for him or her. Writing an option refers to the act of selling an option or shorting an option.
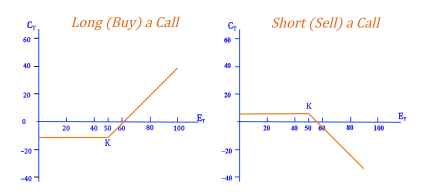
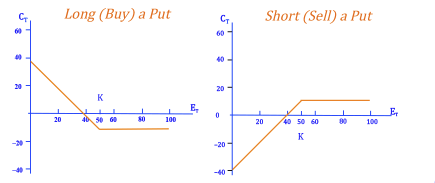
Above we look at the payoff diagrams for buying and selling puts and calls. The payoff diagrams represent options that include an option premium (that is, the purchase price of the option that immediately changes hands).
Where, ST = the value of the stock at expiry (time T)
CT = the value of a call at expiry
K = the exercise price
We can also write the option payoffs at expiration as a formula. For example, the call and put payoffs at expiration for an investor who has bought a call or put are show below.
Call Payoff at Expiration: The payoff for the holder of a call is equal to zero (if the call expires out of the money - ie. the strike price is less than the market price) or the payoff is equal to the difference between the strike price and the market price if the market price goes up.
Put Payoff at Expiration: The payoff for the holder of a put option is equal to zero (if the put expires out of the money - ie. the strike price is greater than the market price), or the payoff is equal to the difference between the strike price and market price if the market price goes down.


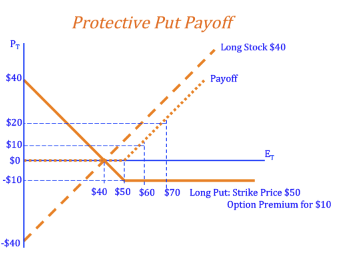
Protective Put
Protective Put: To create a protective put strategy, an investor will buy a put option as well as the underlying stock. A protective put protects investors from loses if the price of the stock they own goes down (they can still sell the stock for the strike price as specified by the put option). However, if the price of the stock goes up, they can keep the stock (or sell it at the new, higher price) and do not have to exercise the put.
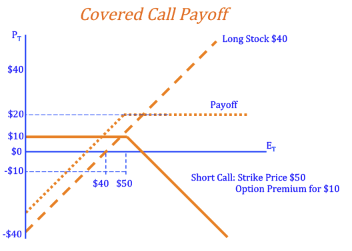
Covered Call
Covered Call: A covered call is a strategy where an investor will buy a stock and sell a call option on the stock at the same time. If the price of the stock goes down, the investor will lose money on the stock; however, the call option will not be exercised and the investor will keep the option premium paid. If the price of the stock goes up, the holder of the call option will exercise their right to buy the stock at the strike price. Because you already own the stock, the exercising of the call will merely offset gains made from the increase in the value of the stock. As long as the stock price does not drop below a certain level, and no matter how much it rises, the investor will make money.
Put-Call Parity
What is you bought a call option on a stock as well as a zero coupon bond?. When we look at the payoff of this strategy at the expiry date (just the payoffs, not including the cost of the strategy) we notice that at any price of the underlying stock, the payoff from this strategy and a protective put are the same. The no-arbitrage principle states that two securities that offer the same future cash flows and have the same risk, must trade at the same price. If this is true, it must cost the same to purchase a protective put (a put option and a stock) as it would to purchase a bond and a call option on that stock.

*We can rearrange this formula to show how other strategies relate. For example, writing a covered call will have the same cost as selling a put and buying a zero coupon bond. We have to be careful to make sure the the exercise dates, lending/borrowing rates, as well as the principle of the bond and the strike price of the option are the same.
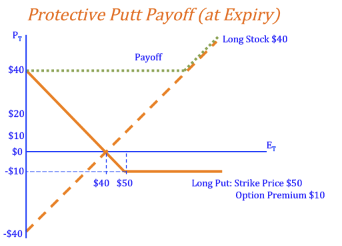
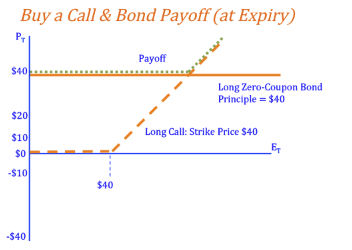
*The two strategies have the same payoffs at expiry.
Photo by Vladislav Babienko on Unsplash
© BrainMass Inc. brainmass.com July 25, 2024, 11:08 am ad1c9bdddf