We can use a binomial options pricing model to value a call option in a hypothetical two-state world. In order to price an option in this model, we look to find a trading strategy that duplicates the payoff of the option. The no-arbitrage principle states that if the payoffs of two trading strategies are equal, the initial costs of both trading strategies must be equal as well. The binomial options pricing model uses a strategy known as "delta hedging." The intuition of this strategy is followed by the Black-Scholes Model as well, and the strategy itself is used in many real world cases by major investment banks who design complex options. Here we look to create a hypothetical portfolio that replicates the payoff of the call, by borrowing money at the risk-free rate and buying the underlying stock. As a result, if you know the cost of borrowing and the price of the stock, an appropriate price for the related call option can be found.
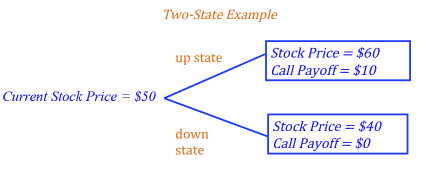
Consider a two-state world. The stock price today is $50. In one-year from now, the stock price will be either $60 or $40. A call option is written on the stock with a one-year expiration date and a $50 exercise price.
Delta Hedging
How much stock?
What we need to do is use the strategy of borrowing and buying a stock to duplicate the risk of a call option. How do we make sure the risk is the same? Imagine a call with an exercise price of $50. If next year the underlying stock is worth $60, the call will have a value of $10. However, if next year the stock is worth only $40, the value of the call is $0. We see that the "swing of the call" (how much the price of the call moves with changes in the stock price) is not the same as the "swing of the stock" (how much the stock price actually changes). By comparing these to swings, we get what we call the delta of the call. We will purchase an amount of stock equal to the delta of the call in our hedging strategy.
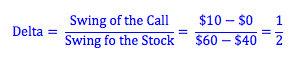
*A one dollar swing in the price of the stock causes a 1/2 dollar swing in the price of the call.
How much to borrow?
If we buy a call option with an exercise price of $50, we will end up with $10 next year if the stock price rises to $60. Therefore, in pricing our strategy, we need to hypothetically borrow an amount that will make the payoff of the borrow-and-buy strategy equal to the payoff of buying the call. If we buy one half of a stock, and the stock price rises to $60 next year, the value of our one half of a stock will be $30. This is $20 more than the value of the call. Therefore, we should borrow an amount today with a future value next year of $20. The present value of $20 (assuming a 10% discount rate) is $18.18 ($20/1.10).
Value of the call.
We know that if two strategies have an equal payoff at expiry their initiatial costs must be the same. Therefore, if we calculate the cost of buying the stock and the amount borrowed, we can find the price of the call.
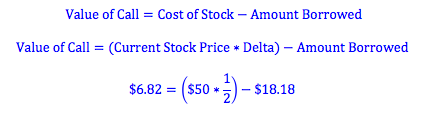
Outcome.
So, we have bought $25 dollars of stock while borrowing $18.18 coming to a total cost of $6.82. If the stock rises to $60 dollars per stock, our stock will rise to $30 (since we bought half a stock). We will now owe $20 for the amount borrowed and so our payoff will be $10. On the other hand, if the stock falls to $40, then our stock will fall to $20 and will be just enough to cover the $20 we owe for the amount we have borrowed. In this case we will have a payoff of $0. Clearly, we have arrived at the same payoff results as the call option and thus satisfying the no-arbitrage condition.
Photo by Immo Wegmann on Unsplash
© BrainMass Inc. brainmass.com July 25, 2024, 6:54 pm ad1c9bdddf