Corporations raise money in two ways: by issuing stocks (equity financing) or by borrowing money (debt financing). Like individuals, businesses may take out mortgages, loans and lines of credit to finance items such as property, plant and equipment, new projects, and inventories as well as to cover expected cash shortfalls. However, unlike individuals, corporations and governments also have the option of issuing bonds. Bonds are a type of security; in essence, bonds are a corporation's promise to pay a specified amount at a future date. Investors buy bonds at an amount equal to the present value of this future payment (or the sum of the discounted future payments expected from the bond). They do this in order to earn interest from the purchase of the bond. Therefore, it is important to be able to price the present value of a bond.
Zero-coupon bonds: A corporation promises to pay a specified amount (typically $1,000) at a future date. This is the face value of the bond. Investors will buy this bond from the corporation at the present value of this one future payment. The present value of a zero coupon bond can be found using the present value formula.
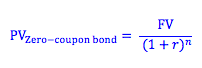
Where PV = the present value, or the price of the bond
FV = face value or future value (the specified amount the corporation has promised to pay at the end of the life of the bond)
r = the interest rate the investor expects to receive
n = the number of periods in the life of the bond
Coupon bonds: A corporation promises to pay a specified amount (the face value - typically $1,000) at a future date as well as periodic payments, typically annually or semi-annually (coupon payments). Corporations will often promise to make periodic payments in order to increase the present value of the bond. As result, investors are willing to pay more for coupon paying bonds than they would if the corporation simply issued zero-coupon bonds. Furthermore, coupon bonds may be seen as less risky since the corporation must meet its interest obligations periodically, rather than defer all payments to the end of the life of the bond. As a result, investors may charge the corporation less interest than they would for a riskier bond. Therefore, coupon bonds have two advantages: corporations get more money today for the bonds they issue, and they may save money on reduced interest rates, making borrowing cheaper. Below is an example of a five-year coupon-paying bond with a 5% discount rate, a face value of $1,000 and an annual coupon payment of $50.
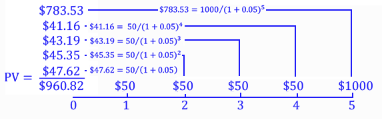
Referring to the diagram above, one will notice that the present value of a coupon bond is equal to the sum of the coupon payments discounted to present value plus the amount of the face value of the bond to be paid at the end of the bond's life, discounted to present value as well.
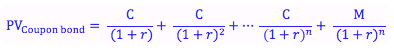
Where C = the amount of the coupon payment
M = the amount of the principle to be repaid
To use this formula, we are required to calculate the present value of each coupon payment. If the bond extends over a longer period of time, these calculations may become tedious. Similarly, if we change the coupon payment or interest rate, all the calculations must be done again. As a result, we often simplify these calculations. If we look closely, we notice that the sum of the coupon payments may simply be found by using the annuity formula.
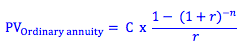
By adding the present value of the future principle payment, we get a simplified formula for the present value of a coupon bond.
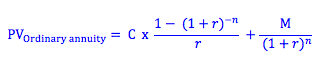
Photo by Austin Distel on Unsplash
© BrainMass Inc. brainmass.com June 30, 2024, 10:06 am ad1c9bdddf