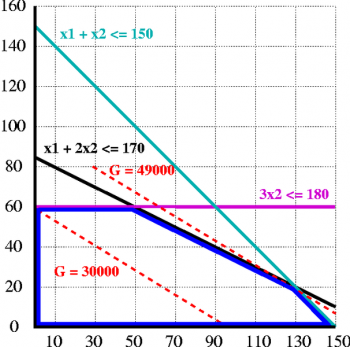
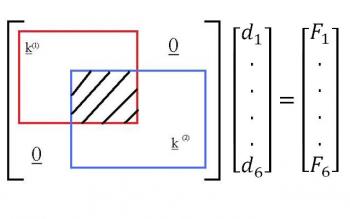
A linear transformation or linear map is a function between two modules that preserves the operations of module addition and scalar multiplication. As a result, it always maps linear subspaces to linear subspaces. For example it maps straight lines to straight lines or a single point. The expression linear operator is often used to refer to a linear map from a vector space to itself. A linear map is a homomorphism of modules. It is a morphism in the category of modules over a given ring.
For example, let V and W be vector spaces over the same field K. A function f: V→W is said to be a linear map if for any two vectors x and y in V and any scalar α in K, then the following two conditions are satisfied.
F(x + y) = f(x) + f(y)
F(αx) = αf(x)
This is equivalent to requiring the same for any linear combination of vectors.
Occasionaly, V and W can be considered to be vector spaces over different fields. It is necessary in these situations to specify which of these ground fields are being used in the definition of linear.
© BrainMass Inc. brainmass.com May 4, 2024, 1:15 am ad1c9bdddf